Trigonometry in Mathematics is defined as a branch, which deals with establishing a relationship between measurement of the length of side and angle of a right triangle. It is also used in the specific area of the circle. The funding of trigonometry was very useful because the computer cannot deal with musical sounds like human ears can do.


The three common, basic, and well-known trigonometry features are height, base, and the hypotenuse. Trigonometry always deals with the relationship between the angles and sides of a right triangle. So, let’s go deeper into the Trigonometry Table in this article.
Learn about the Trigonometry ratio table
The trigonometry ratio table is simply the calculation of the various standard angles that includes various angles like 0-degree angle, 30 degrees, 40-degree angle, 60-degree, 90-degree angle.
They also sometimes calculate the 180-degree angles, 270-degree angles, and 360-degree angles, all in tabular format. We use the table as a reference for calculating trigonometric estimates for various other angles.
The trigonometry ratio table is the table of the values of trigonometric ratio including sins, tangents, cotangent, cousins, cosecant, and secant in between 0 to 360 degrees. We get the values by applying values from 0 to 360 degrees in these trigonometric ratios.
For standard angles such as 0°, 30°, 45°, 60°, and 90°, the trigonometric table can be used to obtain the values of trigonometric ratios. Trigonometric ratios — sine, cosine, tangent, cosecant, secant, cotangent – are listed in a trigonometric table.
Sin, cos, sec, tan, cosec, and cot are the abbreviations for these ratios. In solving trigonometry issues, standard angles are divided by the trigonometric ratios in the table.
Trigonometry is the science of measuring angles and solving issues involving angles.
Trigonometry is a term taken from a Latin word. The relation among the angles and the sides of a triangle is passed on in trigonometry.
Now let us learn the definition of the trigonometric table in detail
The Trigonometric Table consists of a tabular compilation of trigonometric ratio values for various standard angles. These different angles can be like 0°, 30°, 45°, 60°, and 90°, or sometimes it can also be other angles such as 180°, 270°, and 360°. It is assumed easier to estimate the values of such a table and use it as a reference to calculate trigonometric values.
The different values for various other angles are due to the patterns seen within trigonometric ratios and even between angles. The sine function, tan function, cot function, cosine function, sec function, and cosec function are all included in the trigonometric functions.
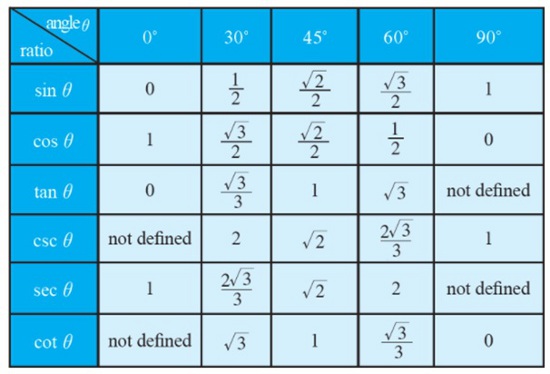

The trigonometric ratios consist of relatable values to each other in it. However, there are some differences while taking the different trigonometric ratios of sin, cosine, secant, cotangent, cosecant, tangent.
The study of length, angles, and their interactions in a triangle is the subject of trigonometry, a branch of mathematics. It’s most commonly linked with a right-angled triangle, in which one of the angles is always 90 degrees.
The trigonometric table comprises the following connected trigonometric ratios: sine, cosine, tangent, cosecant, secant, and cotangent. In a nutshell, these ratios are sin, cos, tan, cosec, sec, and cot.
It is preferable to recall these values and be familiar with the following trigonometric formulae before starting.
So the general trigonometry ratios for a right-angled triangle can be written as;
sinθ = opposite side/hypotenuse
cosθ = adjacent side/hypotenuse
tanθ = opposite side/adjacent side
secθ = hypotenuse / adjacent side
cosecθ = hypotenuse/ opposite side
cotθ = adjacent side/opposite side.
How to Make a Trigonometry Table, let us learn it step by step:
Step 1:
Firstly, create a tabular column with the necessary angles in the top row and all the six trigonometric functions in the first column. It should include sine, cosine, tangent, cosecant, secant, and cotangent.
Step 2:
Calculate the suitable angle’s sine value.
We divide all the values from 0 to 4 by 4, after which we then take the square root to find the value of sin. For instance, to know the value of 0°, write (0/4), i.e. 0, or to get the value of 30°, write (14), i.e. 12.
Step 3:
Calculate the appropriate angle’s cosine value.
The cos values are on the opposite side of the table from the sin angles.
This means that whatever the value of sin (0 – x) degree is, the cos (90 – x) degree is also the same. Divide by 4 in the opposite sequence of sin, i.e., successively from 4, 3, 2, 1, and 0 by 4, and take the square root to determine the value of cos.
For example, to calculate the value of 0°, write (4/4), i.e. 1, or to find the value of 30°, write (34), i.e. 1/32.
Step 4:
Determine the necessary angle’s tangent value.
Sine can be divided by cosine, which equals the tangent. sin x/cos x will be equal to tan x
We divide 30 by cos 30 to get the needed value, which is (12/ (3/2) = ⅓.
Step 5:
Calculate the cot’s worth.
All inverse values of tan can be used to get the value of cot.
As a result, the cost value for each value is 1/tan. Cot x = cos x/sin x, for example. As a result, the related values are simply the tan values’ reciprocal.
Step 6:
Calculate the required angle’s cosecant value.
The inverse of sin on any angle is the value of cosec on that angle. As a result, the reciprocal of the values in sin x will equal the equivalent values.
Step 7:
Find out what the value of sec is.
Any angle’s value of sec is equal to the inverse of that angle’s cos.
Trigonometry is used in a variety of ways.
Oceanography, seismology, meteorology, physical sciences, astronomy, acoustics, navigation, electronics, and other fields have used it.
It can also be used to determine the height of a mountain, the length of a lengthy river, and other similar tasks.
The trigonometric table contains a few crucial points that you need to note down:
- Complementary angles in a trigonometric table, such as 30° and 60°, can be determined using complementary formulas for the various trigonometric ratios.
- In a trig table, the value for various ratios is stated as or “not specified.” The cause for such a table is that a “0” occurs in the denominator when the values are computed, making the value undefined and equivalent to infinity.
- For the values of the particular trig ratios within a trigonometry table, there is a significant change at various places under 180°, 270°, etc. This is because the quadrant has shifted.
Conclusion
Hope you have now understood the fundamentals of the Trigonometry Ratio Table and more in this article.
























